Math in… Holiday Seating
When planning a large holiday celebration, chances are there will be guests who will have a better time if they don’t sit next to one another.
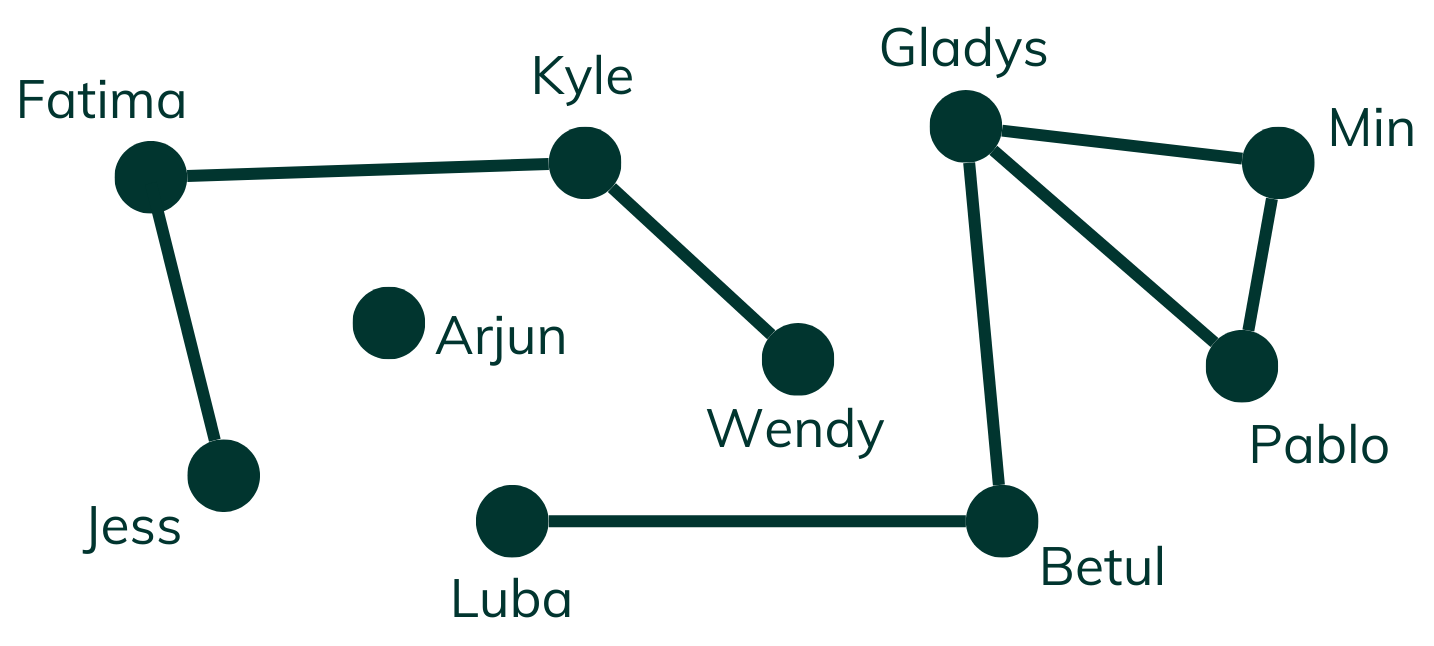
Mathematician Maria Chudnovsky ran into this problem when planning her wedding. Fortunately, Maria is an expert in graph theory, so she had a ready solution. Her solution works like this:
1. Represent each of your attendees as a vertex.
2. Draw an edge between two vertices if those two people should not sit together.
3. Color the vertices so that any two adjacent vertices are different colors. (Don’t use more colors than you have tables!)
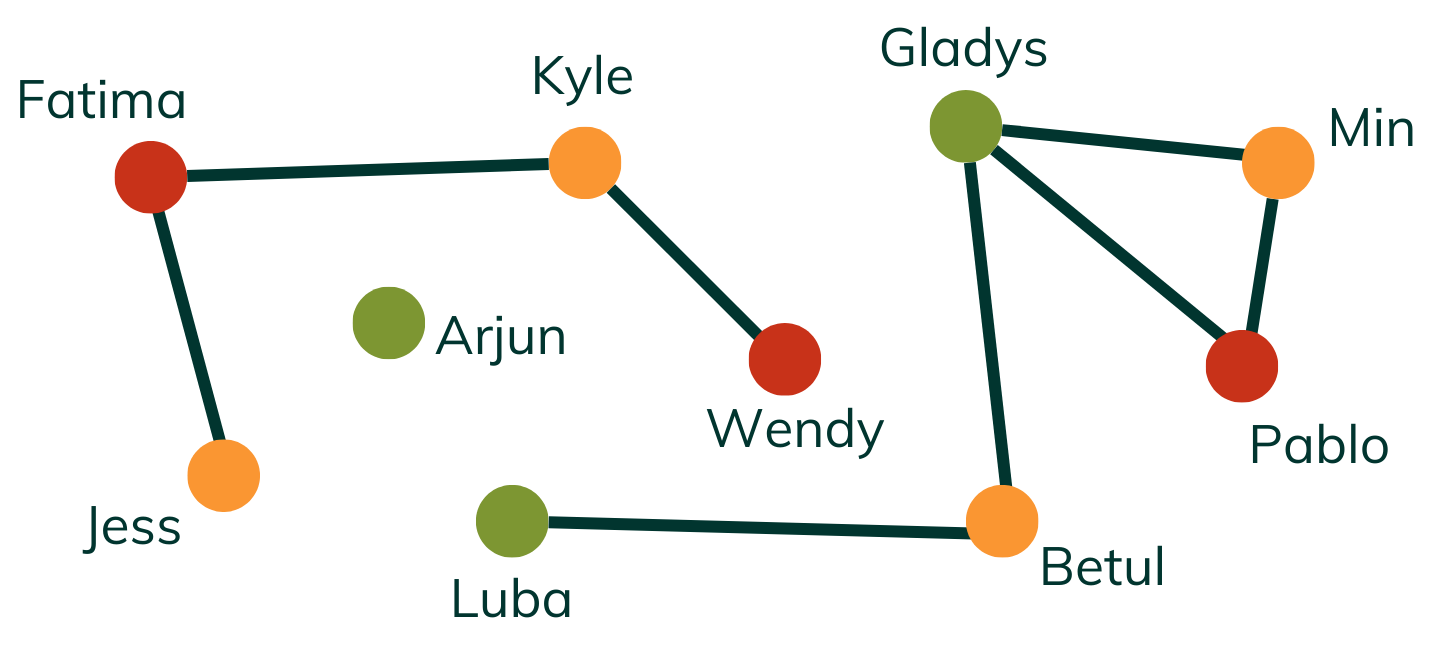
In our example, we ended up with 3 tables:
Fatima, Wendy, Pablo
Arjun, Luba, Gladys
Jess, Kyle, Betul, Min
We can’t do better than 3 tables, since Gladys, Min, and Pablo each need a table away from the other two, but we could have come up with other 3-table solutions.
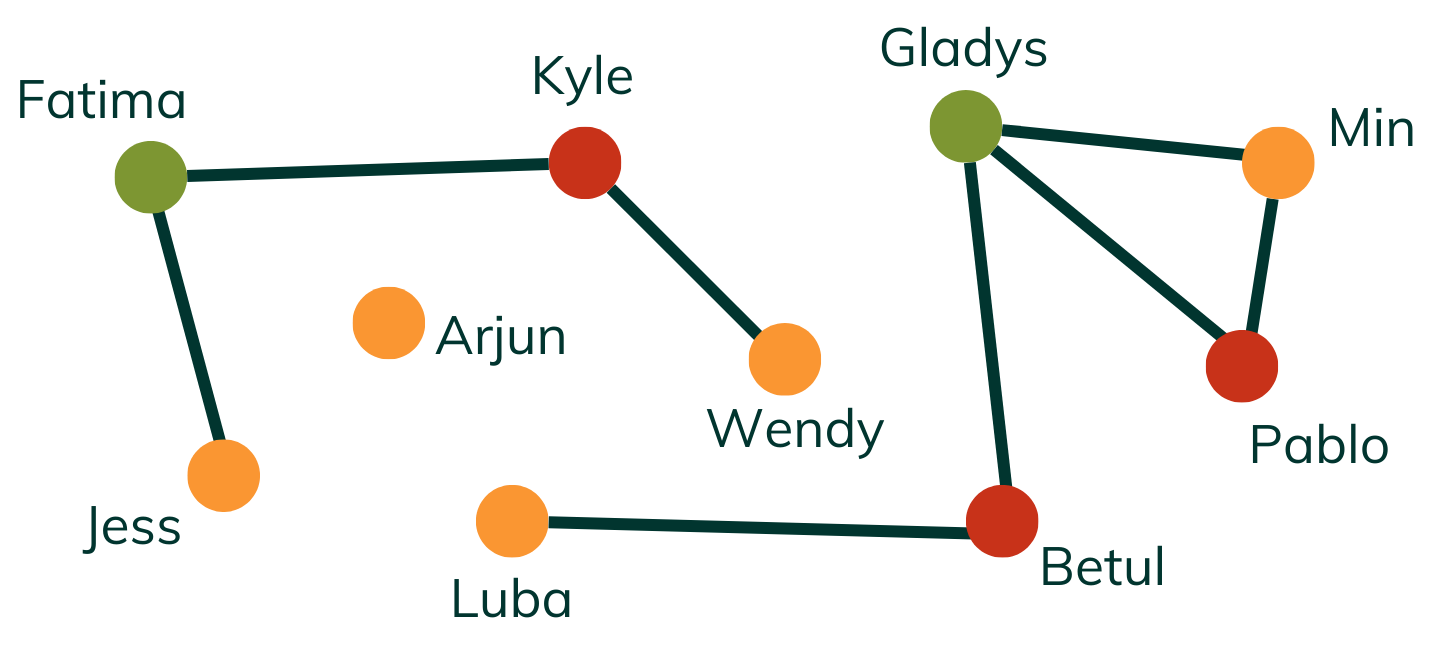
This solution has a small table and a large table:
Fatima, Gladys
Kyle, Betul, Pablo
Jess, Arjun, Wendy, Min, Luba
The smallest number of colors needed to color a graph is its chromatic number. Our example had chromatic number 3.
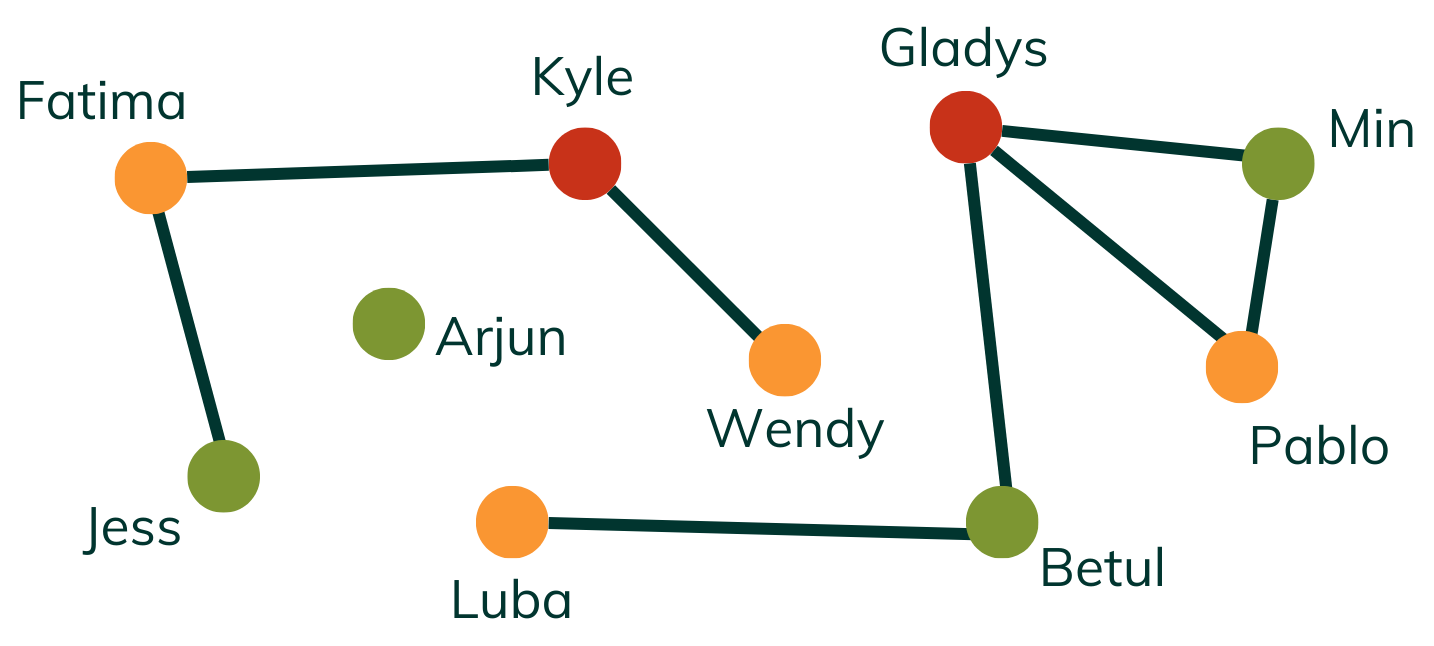
We could look for colorings with other useful restrictions. If we happened to know we had tables that seat four, four, and two, for example, we could try to color four vertices green, four yellow, and two red.
What other math might be helpful when sitting down for a holiday meal?