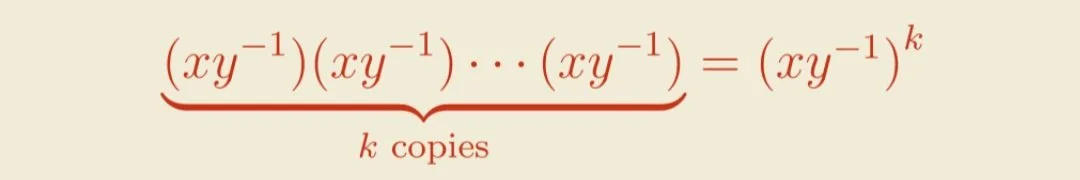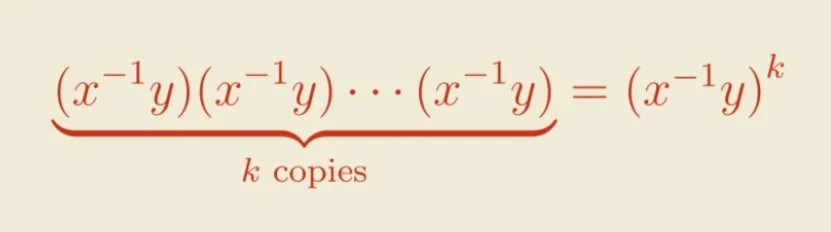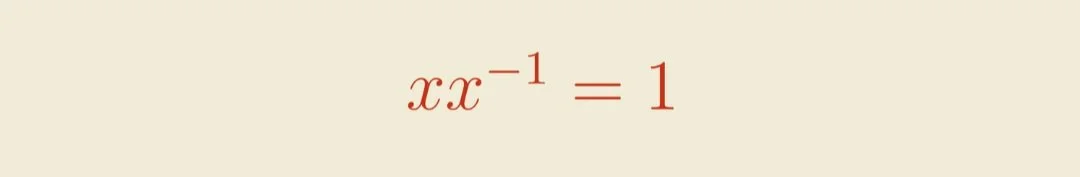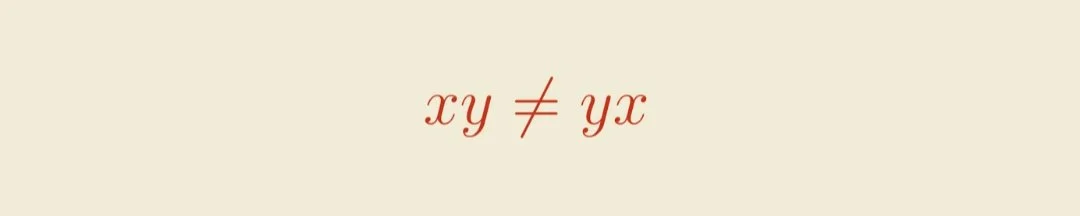Math in… Braids

When you braid hair, cables, ropes, or lanyards, you intertwine strands according to some pattern. The field of math that studies these different intertwining patterns is called braid theory.

In a Dutch braid, the outer strands take turns being crossed under the center strand. This can be tricky to follow because, after the left strand crosses under, it becomes the new center strand. To help keep track of everything, we’ll show the strands with a braid diagram.

In a French braid, the outer strands take turns being crossed over the center strand:

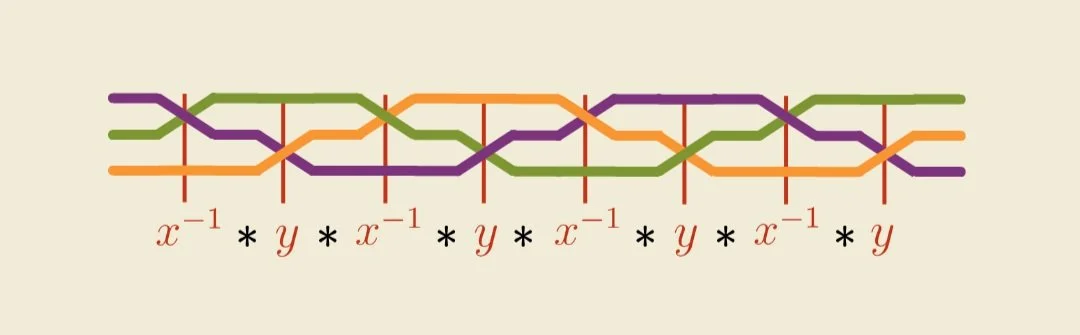
Instead of drawing, we can also use symbols based on whether the center strand crosses over top ( x ), top over center ( x⁻¹ ), bottom over center ( y ), or center over bottom ( y⁻¹ ).

Let’s convert our Dutch braid from pictures to symbols.

If the pattern repeats itself k times, we can write it more succinctly:

Let’s do the same to our French braid diagram.

If we simplify this expression...

And if we simplify further...

These symbols might remind you of algebra, and that’s on purpose!

Part of braid theory is working out the way they interact, in what’s called a braid group.

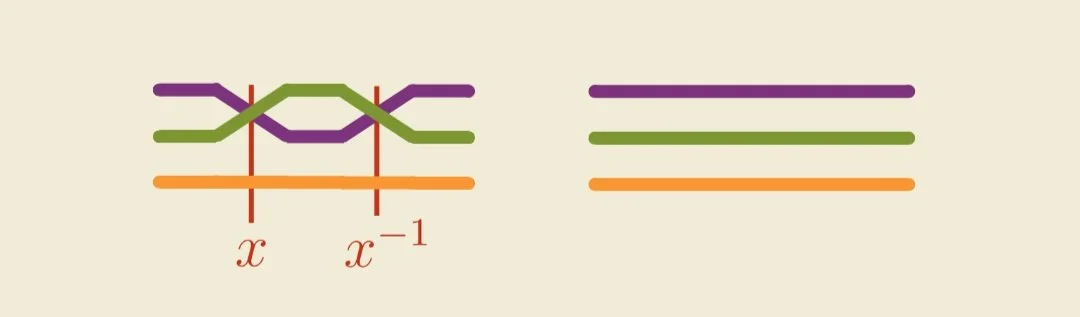
Just like how adding a number and its negative cancels out to zero, an equation like

can mean that x and x⁻¹ cancel each other out.

But not all the rules of algebra apply in braid theory. In algebra, x and y commute, or have the same result regardless of order. But in braid theory, this doesn’t apply! Here,

which seems unusual until you compare the braids.

Where do you see braids in your daily life?