Math in… Packing Oranges

If you’ve ever fidgeted with pennies, you might have noticed you can fit six pennies around a seventh. The kissing number of a circle is six, meaning the largest number of circles that can all simultaneously touch another circle without overlapping it or each other is six.

This arrangement is part of a lattice that turns out to be the most efficient packing of circles possible.

The fraction of a tabletop taken up by pennies in this arrangement is

compared to the square grid packing arrangement’s

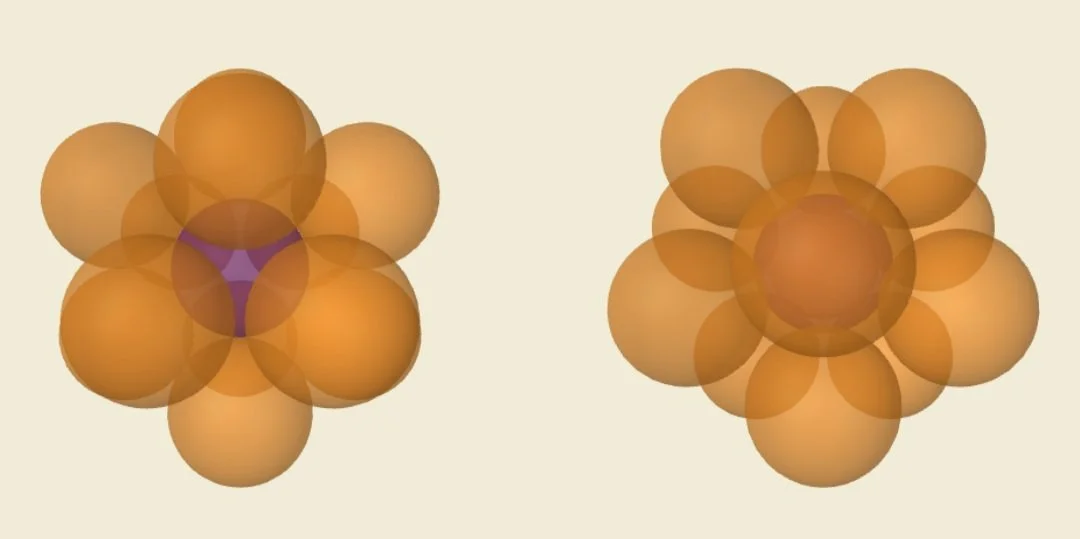
In 3D, the kissing number of a sphere is 12. There are infinitely many different ways to make twelve spheres kiss a thirteenth, since in the arrangement on the right, each orange sphere has a little wiggle room to roll on the surface of the purple sphere without bumping into other orange spheres.

In the arrangement on the right, the orange spheres no longer have wiggle room like they do above.

The last arrangement can be extended into a face-centered cubic packing that is the best you can do in terms of efficiently filling space with spheres. If you had an endless supply of oranges, you could fill about 74% of space with them in this arrangement. If you’ve seen apples or oranges stacked in a pyramid in a grocery store, chances are they were packed like they are on the right.