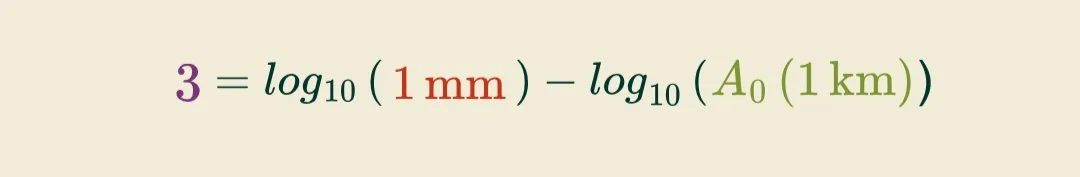Math in… Seismographs

When people talk about earthquakes, they usually describe their size or severity as a number. For example, the United States Geological Survey (USGS) reports that there was a magnitude 6.0 earthquake 272 km west of Bandon, Oregon the day before Halloween.

But what does 6.0 mean?

Early earthquake scores were based on subjective reports of what happened at the epicenter. But since everyone’s perceptions are different, one person might score an earthquake a 3, while another might say 5.

In 1935, physicist Charles Richter used seismograms (readings produced by the recently invented seismograph) to create a scale for objectively measuring earthquakes.

Early seismographs used a pen attached to a suspended mass. As the ground shook, the pen would move relative to the paper, creating a visual record of the seismic waves.

The biggest peak on a seismograph is called the maximum amplitude.

Richter’s magnitude-calculating equation is

which uses the maximum amplitude (or the biggest peak on the seismogram) and a function based on the earthquake data, and adjusted depending on the distance from the epicenter where measurements were taken.

Richter used this equation to show that if you were standing 100 kilometers (62.14 mi) away, and the seismograph drew a peak 1 millimeter tall on the seismogram, the earthquake would have a 3.0 magnitude.

In his equation, Richter used a base-10 logarithm. This means that each whole-number magnitude is ten times more powerful than the number before.

While the Richter scale worked for smaller quakes, readings became less accurate the larger the quakes get.

Today, the USGS uses the moment magnitude scale (MMS), which is also logarithmic.

Whereas the Richter scale has a base-10 logarithm, the moment magnitude scale has a base-32 logarithm. Each whole-number magnitude is 32 times stronger than the one below it!

Have you ever felt an earthquake?