Math in… Corals and Curves
Surfaces you encounter can be curved in some pretty interesting ways. Since a single surface can curve in many different ways, mathematicians typically talk about its curvature at a given point rather than for the surface as a whole.
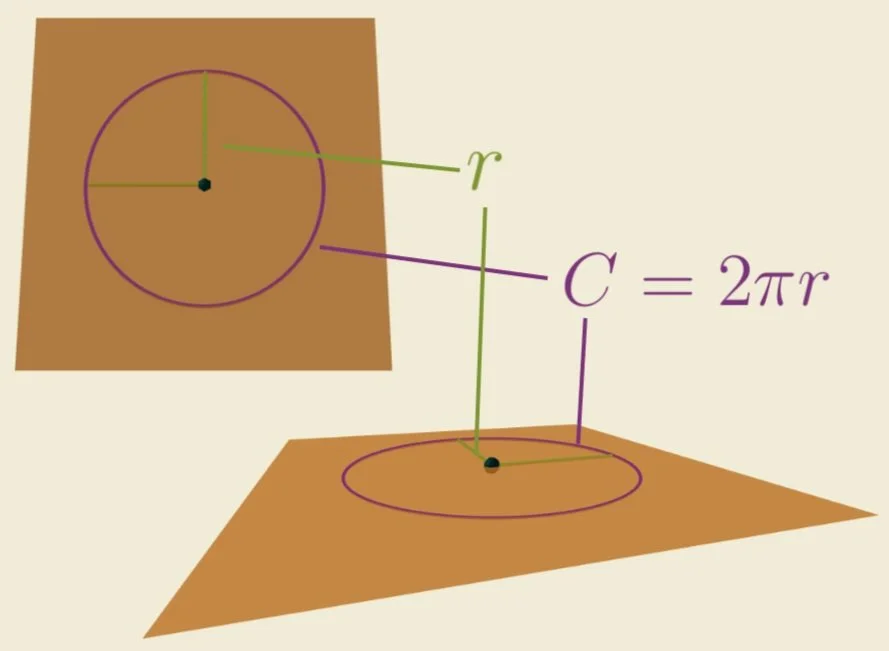
You probably won’t be surprised to learn that flat surfaces have zero curvature at all points. A tabletop or a piece of paper have zero curvature, for example — even if we roll up the paper!
There is a way to compute numerical values (like zero) for curvature using principal curvatures, but a more intuitive way to think is in terms of circles.
At a point of zero curvature, if we create a small circle around that point of radius r, we will find that circle has circumference C = 2πr and area A = πr², as we’ve come to expect.
At a point of positive curvature, a surface will “dome” or “bowl.” If we draw a small circle of radius r about such a point, we’ll find things are smaller than we’d expect: C < 2πr and A < πr².
You might notice that the radius segments actually curve with the surface. This is because they are geodesics, the curves of shortest distance between two points when drawing on the surface.
At a point of negative curvature, a surface will “saddle” or “bunch.” If we draw a small circle of radius r about a point of negative curvature, things are larger than we’d expect: and C > 2πr and A > πr².
Many things you encounter have both points of positive curvature and points of negative curvature!
Which points look more like domes? Which look more like saddles?