Math in… Conveyor Belts

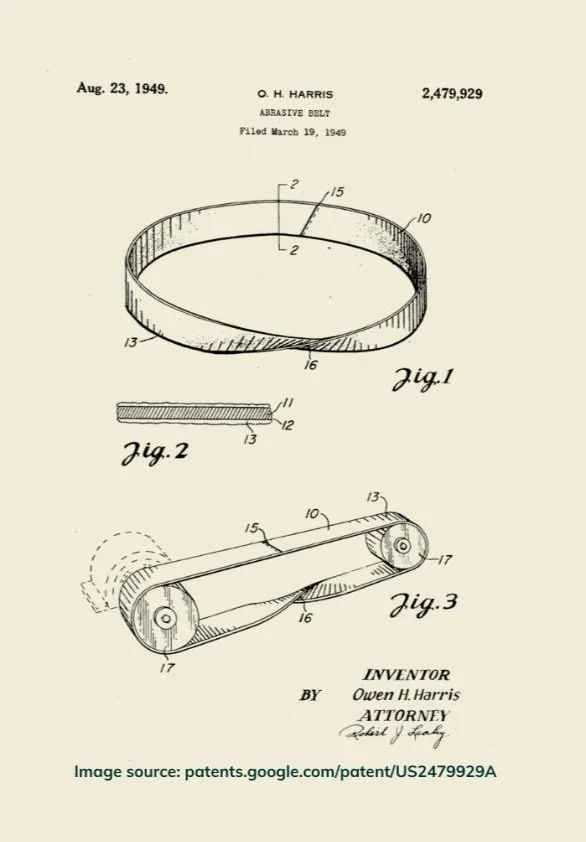
While many things in factories just need to get from one place to another, some might also need to be flipped over along the way. To do this, certain conveyor systems include twists, like the one shown on the left.

One way to think about twists is by starting with a strip of paper and taping the ends together. If you don’t twist before taping, you get a cylinder:

If you twist once before taping, you get a Möbius band:

You can twist a strip as many times as you like!

If you encounter a loop with an unknown number of twists, you can cut it open and count the number twists needed to get back to a cylinder — or model it with paper first and cut that instead!

If you color the two broad faces of a paper strip yellow and green, you’ll notice that after an even number of twists, you will end with a green face and a yellow face.

After an odd number of twists, you will instead see that the green face becomes an extension of the yellow face.

Due to properties that come up as a result of their different “sidednesses,” mathematicians call the even-twisted bands orientable and the odd-twisted bands nonorientable.

The two faces of an untwisted belt tend to wear out at different rates, so some conveyor belt systems have been built with an odd number of twists so that the single belt face experiences uniform wear.

Have you seen a twisted conveyor belt in action? What was it helping to make?